Contoh konsep penggunaan Rekursif
Masalah : Memotong Roti tawar tipis-tipis sampai habis
Algoritma :
1. Jika roti sudah habis atau potongannya sudah paling
tipis maka pemotongan roti selesai.
2. Jika roti masih bisa dipotong, potong tipis dari tepi roti tersebut, lalu lakukan prosedur 1 dan 2 untuk sisa potongannya.
Contoh Fungsi Rekursif
a. Fungsi pangkat
b. Faktorial
c. Fibonancy
d. Menara Hanoi
Fungsi Pangkat
Menghitung 10 pangkat n dengan menggunakan konsep
rekursif.
Secara Notasi pemrograman dapat ditulis :
10^0 = 1 ……............……………………..( 1 )
10^n = 10 * 10^n-1 .....................................( 2 )
Contoh :
10^3 = 10 * 10^2
10^2 = 10 * 10^1
10^1 = 10 * 10^0
10^0 = 1
Faktorial
0! = 1
N! = N x (N-1)! Untuk N > 0
Secara notasi pemrograman dapat ditulis sebagai :
FAKT (0) = 1 ........................................................... (1)
FAKT(N) = N * FAKT (N-1).................................... (2)
Contoh :
FAKT(5) = 5 * FAKT(4)
FAKT(4) = 4 * FAKT(3)
FAKT(3) = 3 * FAKT(2)
FAKT(2) = 2 * FAKT(1)
FAKT(1) = 1 * FAKT(0)
Fibonancy
Deret Fibonancy : 0,1,1,2,3,5,8,13,.........
Secara notasi pemrograman dapat ditulis sebagai :
Fibo (1) = 0 & Fibo (2) = 1 ....................................... (1)
Fibo (N) = Fibo (N-1) + Fibo (N-2) ................................. (2)
Contoh :
Fibo(5) = Fibo(4) + Fibo(3)
Fibo(4) = Fibo(3) + Fibo(2)
Fibo(3) = Fibo(2) + Fibo(1)
Jawabannya:
Fibo(5) = Fibo(4) + Fibo(3) = 7
4 + 3
Fibo(4) = Fibo(3) + Fibo(2) = 4
3 + 1
Fibo(3) = Fibo(2) + Fibo(1) = 3
1 + 0
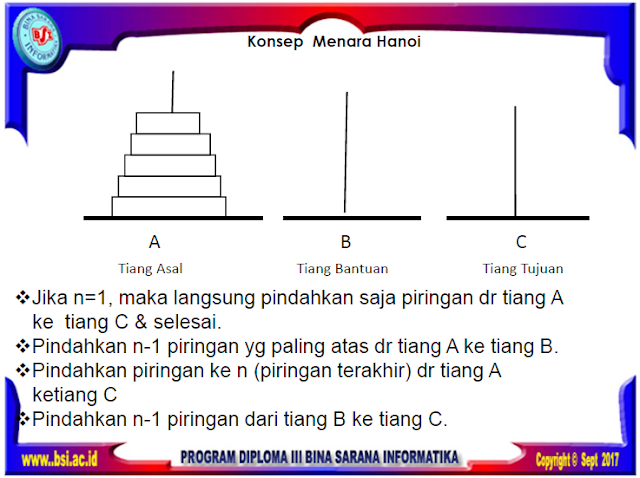
Langkah pemindahan tersebut diatas dapat diubah dengan notasi sebagai berikut:
Menara (n,asal,bantu,tujuan)
- Utk jml piringan n>1 dpt dibagi menjadi 3 notasi penyelesaian
- Menara (n-1, Asal,Tujuan, Bantu);
- Menara (n, Asal, Bantu, Tujuan); atau Asal > Tujuan;
- Menara (n-1, Bantu, Asal, Tujuan);
Rumus Langkah Pemindahan :
2^N-1
N = Jumlah Piringan
Download Data: Struktur Rekursif
Sekian pembahasan dari Struktur Rekursif. Saya Mr.JAR mengucapkan terima kasih dan Semoga bermamfaat.


0 komentar:
Post a Comment